Inhalt
- Der erste Kontakt
- Mandelbrot Kata
- Der Algorithmus in C++
- Mathematik der Komplexen Zahlen in C++
- Optimierungen
- Datentypen
- Multithreading
- Alternativen in C++
- SIMD
- Fragen / Code-guck
Die Mandelbrot Menge in C++ (alles außer SIMD)
Sven Johannsen
C++ User Group NRW
Düsseldorf 2016-01-20
Normalerweise stellen wir an dieser Stelle irgendwas zum Thema C++ vor und zeigen an Code-Beispielen was man damit machen kann.
Dieser Vortrag zeigt einen fertigen Algorithmus aus der C++-Brille.
Durch den gewählten Algorithmus ist der Vortrag etwas "Fließkomma"-lastig. Die Themen Vererbung, Polymorphie und Smart-Pointer fehlen ganz und Templates werden nur am Rand erwähnt.
Ich bitte dies zu entschuldigen.
(from Benoid B. Mandelbrot, 1983)
(from Benoid B. Mandelbrot, 1983)
Ende der 80er tauchten tolle Bilder auf, die mit einer einfachen Formel erzeugt wurden.
z=z^2+c
Mit dieser Formel und "quadratic dynamics" sollten Computer diese Bilder erzeugen können.
Ich hatte keine Idee wie das gehen sollte!
(Spektrum der Wissenschaft, Sonderheft 8, Computer Kurzweil III, 1989)
Ein erster Lichtblick:
n <- 0
WHILE n < 100 und Betrag(z) < 2
z = z^2 + c
n <- n + 1
Färbe den Aufpunkt
für Programmiersprachen, die mit Komplexen Zahlen umgehen können.
Variante für andere Programmiersprachen
n <- 0
WHILE n < 100 und x^2 + y^2 < 4
xx <- x^2 - y^2 + a
y <- 2xy + b
x <- xx
n <- n+1
Färbe den Aufpunkt
Der Algorithmus enthält die Variablen x und y, die jedoch nichts mit den Bildschirm Koordinaten zu tun haben;
n wird mit 0 initialisiert, x, y und xx nicht.
(Die Transformation der Bildschirmkoordinaten zu a und b wird getrennt beschrieben.)
Pascal Quelltext von 1991. (Quelle: wahrscheinlich c't?)
Großartig für AT286 ohne 287 Coprozessor
{$B-,R-,I-,S-,X+}
USES Graph,Crt;
CONST
MaxTiefe = 100;
Ymin = -1200;
Ymax = 1200;
Xmin = -2000;
Xmax = 650;
Norm = 1000;
VAR
MaxX,MaxY,HalbY : INTEGER;
FUNCTION iterate(nx, ny : LONGINT) : LONGINT;
VAR
tiefe : INTEGER;
X,Y,Xalt,
Xp,Yp : LONGINT;
BEGIN
Xp := ((Xmax - Xmin) * nx) DIV (MaxX -1) + Xmin;
Yp := ((Ymax - Ymin) * ny) DIV (MaxY -1) + Ymin;
tiefe := 0;
x := 0;
y := 0;
WHILE (tiefe < MaxTiefe) AND ((X * X + Y * Y) < 4000000) DO BEGIN
Xalt := x;
X := (X * X - Y * Y) DIV NORM +Xp;
Y := (2 * Xalt * Y) DIV NORM +Yp;
INC(tiefe);
END;
iterate := tiefe;
END;
VAR
Gd, Gm : INTEGER;
nx,ny,i : INTEGER;
BEGIN
Gd := VGA;
Gm := VGAHi;
InitGraph(Gd,Gm,'\ps\tp\bgi');
MaxX := GetMaxX;
MaxY := GetMaxY;
HalbY := MaxY DIV 2;
nx := 0;
WHILE nx < MaxX DO BEGIN
ny := 0;
WHILE ny < HalbY DO BEGIN
i := Iterate(nx,ny) MOD 16 + 1;
PutPixel(nX,nY,i);
PutPixel(nX,MaxY-nY-4,i);
INC(ny);
END;
INC(nx);
IF KeyPressed THEN nx := MaxX;
END;
ReadKey;
CloseGraph;
END.
''Setze den Mandelbrot Algorithmus in der neuen Programmiersprache um.''
(Mein persönliches Kata, für den ersten Kontakt mit einer neuen Programmiersprache)
start = os.clock()
disp_width = 80
disp_height = 25
scale_real = 3.0 / disp_width
scale_imag = 3.0 / disp_height
line = ""
for j = 1, disp_height do
line = ""
for i = 1, disp_width do
x = (i * scale_real) - 1.8
y = (j * scale_imag) - 1.5
u = 0.0
v = 0.0
u2 = 0.0
v2 = 0.0
iter = 0
while (u2 + v2 < 4.0) and (iter < 100) do
v = 2 * v * u + y
u = u2 - v2 + x
u2 = u*u
v2 = v*v
iter = iter + 1
end
if iter < 10 then c = ' '
elseif iter < 20 then c = '.'
elseif iter < 30 then c = 'o'
elseif iter < 50 then c = '*'
elseif iter < 70 then c = 'x'
elseif iter < 90 then c = 'X'
then c = '@'
end
line = line .. c
end
print(line)
line = ""
end
ende = os.clock()
print("Dauer:" .. ende - start .. "sek.")
Lernziele:
Wenn man die gleiche Aufgabe mit verschieden Programmiersprachen löst, kann man diese vergleichen.
| Sprache | Version | i5-5200U (Linux) |
|---|---|---|
| python | (3.4.3) | 104.8 KPixel/s |
| lua | (5.2.3) | 133.5 KPixel/s |
| nodejs | (0.10.25) | 11.0 MPixel/s |
| java | (1.7.0.79) | 12.9 MPixel/s |
| C++ | (GCC 4.8.5) | 13.1 MPixel/s |
Eine Implementierung in C++
(basierend auf dem Artikel von 1989)
n <- 0
WHILE n < 100 und Betrag(z) < 2
z = z^2 + c
n <- n + 1
Faerbe den Aufpunkt
int pixel(double re, double im)
{
std::complex<double> z{ 0. }, c{ re, im };
int n{ 0 };
while (n < 100 && std::abs(z) < 2.0) {
z = z * z + c;
++n;
}
return n;
}
Bildschirm-Koordinaten in eine Komplexe Zahlenebene transponieren.
const int disp_width = 179, disp_height = 80;
const double start_real = -1.8, start_imag = -1.5;
const double scale_real = 3.0 / disp_width;
const double scale_imag = 3.0 / disp_height;
for (int j = 1; j < disp_height; ++j) {
for (int i = 1; i < disp_width; ++i) {
const double re = start_real + i * scale_real;
const double im = start_imag + j * scale_imag;
const int iter = pixel(re, im);
cout << transform(iter);
}
cout << '\n';
}
Bildschirmauflösung 178x79
Wertebereich: [-1.8..1.2; -1.5..1.5]
i,j: Bildschirmkoordinaten
re,im: Korrdinaten im einer Komplexen Ebende
Das Ergebnis muss in "Farben" umgewandelt werden.
char transform(int iter)
{
if (iter < 10) return ' ';
if (iter < 20) return '.';
if (iter < 30) return 'o';
if (iter < 50) return '*';
if (iter < 70) return 'x';
if (iter < 90) return 'X';
return '@';
}
Projekt: demo
Datei: SimpleExample.h
(check test.cpp)
2 alternative Lösungen ohne std::complex<T>
// (1 von 1989)
float u{ 0 }, v{ 0 };
int iter{ 0 };
while (u*u + v*v < 4.f && iter < 100) {
const float uu = v*v - u*u + re;
u = 2.f * u*v + im;
v = uu;
++iter;
}
// (2 intel, ...)
float u{ 0 }, v{ 0 }, u2{ 0 }, v2{ 0 };
int iter{ 0 };
while (u2 + v2 < 4.f && iter < 100) {
v = 2.f * v * u + im;
u = u2 - v2 + re;
u2 = u*u;
v2 = v*v;
++iter;
}
Windows 10 - Visual Studio (64bit)
Intel(R) Core(TM) i5-5200U CPU @ 2.20GHz
| Datentype | VS2013 | VS2015 |
|---|---|---|
| complex<float> | 1.9 MPixel/s | 10.8 MPixel/s |
| complex<double> | 8.0 MPixel/s | 8.0 MPixel/s |
| float (1) | 12.8 MPixel/s | 12.3 MPixel/s |
| double (1) | 12.8 MPixel/s | 12.3 MPixel/s |
| float (2) | 12.3 MPixel/s | 12.6 MPixel/s |
| double (2) | 12.8 MPixel/s | 12.5 MPixel/s |
Mint Linux 17.2 - GCC 4.8.5
Intel(R) Core(TM) i5-5200U CPU @ 2.20GHz
| Datentype | -O3 | -O3 -ffast-math |
|---|---|---|
| complex<float> | 2.3 MPixel/s | 12.9 MPixel/s |
| complex<double> | 6.6 MPixel/s | 13.0 MPixel/s |
| float (1) | 14.1 MPixel/s | 12.6 MPixel/s |
| double (1) | 14.0 MPixel/s | 12.5 MPixel/s |
| float (2) | 13.5 MPixel/s | 14.1 MPixel/s |
| double (2) | 13.4 MPixel/s | 14.1 MPixel/s |
Vereinfachte Klasse für Komplexe Zahlen
template<typename FLOAT_TYPE>
struct Complex {
typedef FLOAT_TYPE value_type;
FLOAT_TYPE re_;
FLOAT_TYPE im_;
FLOAT_TYPE real() const { return re_; }
FLOAT_TYPE imag() const { return im_; }
};
Complex<double> z = { 0. }, c = { re, im };
Mathematische Operatoren
template<typename FLOAT_TYPE>
inline Complex<FLOAT_TYPE> operator+(const Complex<FLOAT_TYPE>& l,
const Complex<FLOAT_TYPE>& r)
{
return Complex<FLOAT_TYPE>{l.re_ + r.re_,
l.im_ + r.im_ };
}
template<typename FLOAT_TYPE>
inline Complex<FLOAT_TYPE> operator*(const Complex<FLOAT_TYPE>& l,
const Complex<FLOAT_TYPE>& r)
{
return Complex<FLOAT_TYPE>{ l.re_ * r.re_ - l.im_ * r.im_,
l.re_ * r.im_ + l.im_ * r.re_ };
}
z = z * z + c;
Absoluter Betrag.
template<typename T>
T abs(const Complex<T>& z)
{
return sqrt(z.re_*z.re_ + z.im_*z.im_);
}
while (abs(z) < 2.0 && iter < 100) {
...
}
mit dem Mandelbrot Algorithmus (z = z * z + c)
3 kleine Beispiele für:
(Koordinaten auf der Komplexen Zahlenebene)
Startwert c = (0, 0i)
Complex z{ 0 }, c{ 0.0, 0.0 };
while (std::abs(z) < 2.0 && iter < 100) {
z = z * z + c;
++iter;
}
z = (0, 0i)*(0, 0i) + (0, 0i) = (0, 0i)
bei allen Berechnungen
=> Endlosschleife ohne die Abbruchbedingung iter<100
Startwert c = (-2, 0i)
Complex z{ 0 }, c{ -2.0, 0.0 };
while (std::abs(z) < 2.0 && iter < 100) {
z = z * z + c;
++iter;
}
z = (0, 0i)*(0, 0i) + (-2, 0i) = (-2, 0i)
abs(-2, 0i) = 2
abs(z) < 2.0 ist im ersten Durchgang erfüllt.
iter == 1
In der ersten Iteration erhält z den Wert von c.
Die Kreisformel definiert einen Grenzwert um die Mandelbrotmenge:
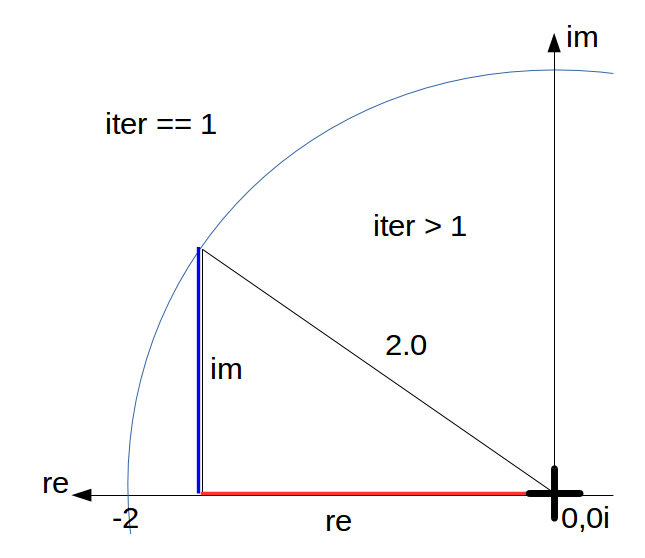
z' = z*z + (-1, 0i)
z^2 = z*z
| iter | z | z^2 | c | z' |
|---|---|---|---|---|
| 1 | ( 0.0, 0.0i) | (0.0, 0.0i) | (-1.0, 0.0i) | (-1.0, 0.0i) |
| 2 | (-1.0, 0.0i) | (1.0, 0.0i) | (-1.0, 0.0i) | ( 0.0, 0.0i) |
| 3 | ( 0.0, 0.0i) | (0.0, 0.0i) | (-1.0, 0.0i) | (-1.0, 0.0i) |
| 4 | (-1.0, 0.0i) | (1.0, 0.0i) | (-1.0, 0.0i) | ( 0.0, 0.0i) |
Der Wert von z wechselt zwischen (0, 0i) und (-1, 0i) und erreicht nie abs(z) >= 2.
=> iter == 100

|
|
while (std::abs(z) < 2.0 && iter < 100) {
z = z * z + c;
++iter;
}
Was passiert, wenn man die Konstanten 100 (maximale Iterationen) und 2.0 (Escape Radius) anpasst?
http://mathworld.wolfram.com/MandelbrotSet.html
Neben den schönen Bildern gilt die Hauptfrage bei der Mandelbrotmengen-Berechnen nach der Performance. Wie kann man die Bilder möglichst schnell berechnen?
while Schleifesqrt, abs) ...
std::complex z{0.}, c{x,y};
int iter{0};
while ((std::abs(z) < 2.0) && (iter < 100)) {
z = z * z + c;
++iter;
}
...
while -Abfrage ist immer true beim ersten Test!
// `while` - loop
int pixel(double x, double y)
{
std::complex z{0.}, c{x,y};
int iter{0};
while ((std::abs(z) < 2.0) && (iter < 100)) {
z = z * z + c;
++iter;
}
return iter;
}
// `do` - loop
int pixel(double x, double y)
{
std::complex z{0.}, c{x,y};
int iter{0};
do {
z = z * z + c;
++iter;
} while ((std::abs(z) < 2.0) && (iter < 100));
return iter;
}
Wie kann die Optimierung gemessen werden?
| Datentype | VS2015 | 1 Iter. | GCC 4.8 | 1 Iter. |
|---|---|---|---|---|
| do/while (float) | 12.5 | 344.6 | 13.4 | 253.2 |
| do/while (double) | 12.3 | 346.3 | 13.4 | 254.4 |
| while (float) | 12.8 | 349.8 | 13.4 | 253.8 |
| while (double) | 12.7 | 348.1 | 13.4 | 253.5 |
| for (float) | 12.3 | 353.4 | 13.5 | 253.1 |
| for (double) | 12.5 | 349.7 | 13.4 | 253.6 |
Alle Werte in MPixel/s
GCC 4.8.5 auf Mint Linux 13.2, VS2015 unter Windows 10
Was bringt es Schleifen auszurollen? (loop unrolling)
| Compiler/data type | no | 5 | 10 | full |
|---|---|---|---|---|
| GCC 4.8.5 (float) | 13.5 | 13.6 | 13.7 | 13.2 |
| GCC 4.8.5 (double) | 13.5 | 13.6 | 13.6 | 13.2 |
| VS2013 (float) | 12.3 | 13.1 | 13.1 | 13.1 |
| VS2013 (double) | 12.8 | 13.1 | 13.1 | 12.7 |
| VS2015 (float) | 12.5 | 13.1 | 13.2 | 13.1 |
| VS2015 (double) | 12.6 | 13.1 | 13.2 | 12.6 |
Alle Werte in MPixel/s
GCC auf Mint Linux 13.2, VS2015 unter Windows 10
template<typename FLOAT_TYPE, int MAX_ITER>
struct Pixel
...
do {
v = 2.0 * v * u + im;
u = u2 - v2 + re;
u2 = u*u;
v2 = v*v;
++iter;
} while (u2 + v2 < 4.0 && iter < MAX_ITER);
...
Welches Literal soll für "2.0" verwendet werden?
"2" "2.f" "2.0"| Initialisierung | GCC 4.8.5 | VS2015 |
|---|---|---|
| float 2 | 372 ns | 654 ns |
| double 2 | 371 ns | 585 ns |
| float 2.f | 371 ns | 530 ns |
| double 2.f | 372 ns | 414 ns |
| float 2.0 | 638 ns | 623 ns |
| double 2.0 | 372 ns | 414 ns |
| float template type | 372 ns | 418 ns |
| double template type | 372 ns | 415 ns |
Alles aus der Schleife heraus ziehen was möglich ist!
for (int j = 1; j < disp_height; ++j) {
for (int i = 1; i < disp_width; ++i) {
const double re = i * scale_real - 1.8;
const double im = j * scale_imag - 1.5; // (A)
const int iter = pixel(re, im);
...
}
}
for (int j = 1; j < disp_height; ++j) {
const double im = j * scale_imag - 1.5; // (A)
for (int i = 1; i < disp_width; ++i) {
const double re = i * scale_real - 1.8;
const int iter = pixel(re, im);
...
}
}
Startwert vs. Addition
for (int j = 1; j < disp_height; ++j) {
const double im = y1 + j * scale_imag; // (1)
for (int i = 1; i < disp_width; ++i) {
const double re = x1 + i * scale_real; // (2)
const int iter = pixel(re, im);
...
}
}
double im = y1; // (1a)
for (int j = 1; j < disp_height; ++j) {
im += scale_imag; // (1b)
double re = x1; // (2a)
for (int i = 1; i < disp_width; ++i) {
re += scale_real; // (2b)
const int iter = pixel(re, im);
...
}
}
Von Startwert neu berechnen: Der Fehler bleibt konstant / in der gleichen Größenordnung.
for(int j = 0; ...) {
const float im = j * scale_imag + starty;
...
}
Bei der Addition summieren sich die numerischen Fehler auf!
float im = starty;
for(int j = 0; ...) {
im += scale_imag;
...
}
z.B. abs() bzw. sqrt():
do {
...
} while ((std::abs(z) < 2.0) && (iter < 100));
do {
...
} while ((z.imag() * z.imag() + z.real() * z.real() < 4.0) && (iter < 100));
| Benchmark | GCC 4.8.5 | VS2015 |
|---|---|---|
| BM_cmplx_abs | 29 ns | 77 ns |
| BM_cmplx_hypot | 13 ns | 9 ns |
| BM_cmplx_sqrt | 13 ns | 6 ns |
| BM_cmplx_square | 8 ns | 3 ns |
| BM_cmplx_empty | 7 ns | 3 ns |
| BM_float_hypot | 19 ns | 9 ns |
| BM_float_sqrt | 13 ns | 7 ns |
| BM_float_square | 8 ns | 3 ns |
| BM_float_empty | 7 ns | 3 ns |
std::sqrt(re*re+im*im) >= 2.0 ist merklich teuer als re*re+im*im >= 4.0
std::hypot() ist teurer als std::sqrt() wegen zusätzlicher Checks.
std::abs(std::complex) ist teurer als std::hypot() wegen zusätzlicher NaN, Unendlich und Stabilitäts-Checks.
Vergleiche verschiedene Datentypen
| Data type | GCC | VS2015 |
|---|---|---|
| float | 13.5 MPixel/s | 12.6 MPixel/s |
| double | 13.4 MPixel/s | 12.5 MPixel/s |
| long double | 8.5 MPixel/s | 12.5 MPixel/s |
| int32_t | 8.1 MPixel/s | 8.0 MPixel/s |
| int64_t | 8.2 MPixel/s | 8.1 MPixel/s |
| complex<float> | 2.3 MPixel/s | 10.8 MPixel/s |
| complex<double> | 6.6 MPixel/s | 8.0 MPixel/s |
int so langsam?Wieso ist int langsamer als Fließkomma-Typen?
int so langsam?int ist nicht das Problem - es is die Division-Korrektur!
| Datentyp | 64 bit | 32 bit |
|---|---|---|
| float | 12.6 MPixel/s | 12.5 MPixel/s |
| double | 12.5 MPixel/s | 12.9 MPixel/s |
| int 32 bit | 8.0 MPixel/s | 7.5 MPixel/s |
| int 64 bit | 8.1 MPixel/s | 1.2 MPixel/s |
| float (div) | 6.0 MPixel/s | 6.0 MPixel/s |
| double (div) | 5.3 MPixel/s | 5.4 MPixel/s |
| float (mul) | 9.6 MPixel/s | 9.5 MPixel/s |
| double (mul) | 9.5 MPixel/s | 9.3 MPixel/s |
long double so langsam (auf Linux)?Der GCC erzeugt für alle Datentypen schnelleren Code - außer für long double. Warum?
long double so langsam (auf Linux)?Linux: sizeof(long double) == 16
Windows (Visual Studio) sizeof(long double) == 8
long doubleSSE unterstützt nur 4 und 8 Byte Fließkommatypen.
long double muss auf der FPU gerechnet werden (Linux).
Die SSE Recheneinheiten sind schneller als die FPU.
Kein Problem - AVX ist viel schneller
Nutze GCC mit -ffast-math
| Data type | GCC 4.8.5 | -ffast-math | VS 2015 |
|---|---|---|---|
| float | 13.3 | 14.1 | 12.6 |
| double | 13.2 | 14.1 | 12.5 |
| std::complex (float) | 2.3 | 12.9 | 10.8 |
| std::complex (double) | 6.6 | 13.0 | 8.0 |
| mandel::complex (float) | 13.5 | 12.9 | 10.8 |
| mandel::complex (double) | 13.2 | 12.9 | 10.7 |
Alle Werte in MPixel/s
Siehe:
beide: Herb Sutter.
Äußere Schleife parallelisieren:
#pragma omp parallel for
for (int j = 0; j < height; ++j) {
const FLOAT_TYPE y = (j * dy) + y1;
for (int i = 0; i < width; ++i) {
const FLOAT_TYPE x = (i * dx) + x1;
auto iter = pixel(x, y);
...
}
}
#pragma omp OpenMP Befehlparallel for Parallele for-Schleife, muss vor einer for Anweisung stehenÄußere Schleife durch tbb::parallel_for ersetzen.
tbb::parallel_for(int(0), int(height), [&](int j) {
const FLOAT_TYPE y = (j * dy) + y1;
for (int i = 0; i < width; ++i) {
const FLOAT_TYPE x = (i * dx) + x1;
const auto iter = pixel(x, y);
...
}
});
Der Schleifen-body (die innere Schleife) wird als Lambda formuliert.
#pragma omp parallel for
for (int j = 0; j < height; ++j) {
...
}
tbb::parallel_for(int(0), int(height), [&](int j) {
...
});
Der innere Teil (...) ist in beiden Varianten gleich.
| Methode | float | double |
|---|---|---|
| Sequentiell | 12.6 MPixel/s | 12.6 MPixel/s |
| OpenMP | 22.8 MPixel/s | 23.1 MPixel/s |
| Intel TBB | 39.2 MPixel/s | 39.3 MPixel/s |
| std::futures | 37.3 MPixel/s | 37.5 MPixel/s |
Visual Studio 2015.
2 Ergebnisse:
Intel Core i7-2860QM 2.5 GHz 4 Kerne, HyperThreading (8 Hardware-Threads)
| - | Ohne HT | Mit HT |
|---|---|---|
| Ohne TB | 9.0 35.5 (x3.94) |
9.0 58.9 (x6.54) |
| Mit TB | 12.7 (x1.41) 46.5 (x3.66) |
12.7 (x1.41) 76.8 (x6.04) |
HT: Hyper-Threading
TB: Intel Turbo Boost
Single threaded vs TBB
OpenMP verwendet als default(*) einen statischen Scheduler, dazu wird der Bereich in gleich große Blöcke aufgeteilt.
Der dynamischen Scheduler verteilt die Arbeit "gleichmäßig" auf die Kerne.
#pragma omp parallel for schedule(dynamic)
(*) unspezifiziert. (aber alle mir bekannten Compiler nutzen den statischen Scheduler als default Scheduler)
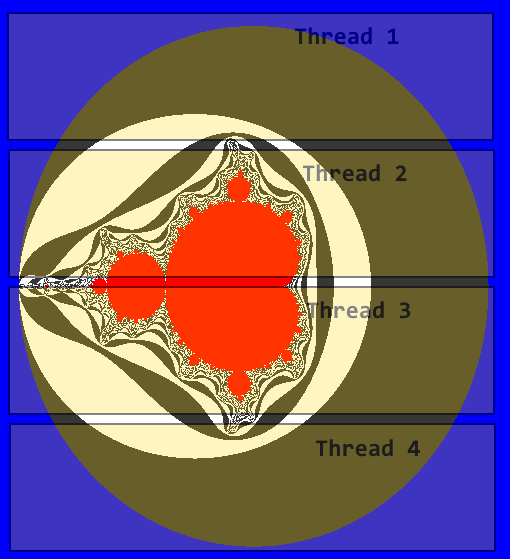
| Methode | float | double |
|---|---|---|
| Sequentiell | 12.6 MPixel/s | 12.6 MPixel/s |
| OpenMP static | 22.8 MPixel/s | 23.1 MPixel/s |
| OMP dynamic | 40.6 MPixel/s | 39.6 MPixel/s |
| Intel TBB | 39.2 MPixel/s | 39.3 MPixel/s |
| std::futures | 37.3 MPixel/s | 37.5 MPixel/s |
Schleifen und Rekursion sind das Gleiche - Man kann sie einfach ineinander überführen.
aus der Sicht eines Mathematikers
Kann man den Mandelbrot Mengen Algorithmus effizient rekursiv programmieren?
int pixel_detail(int iter, COMPLEX_TYPE z,
const COMPLEX_TYPE c, const int max_iter)
{
if (iter < max_iter) {
z = z * z + c;
if ((z.imag() * z.imag() + z.real() * z.real() < FLOAT_TYPE(4.0)))
return pixel_detail(iter + 1, z, c, max_iter);
}
return iter;
}
Da war doch noch was Endrekursion bzw. tail recursive optimization.
Eine rekursive Funktion f ist endrekursiv (englisch tail recursive; auch endständig rekursiv, iterativ rekursiv, repetitiv rekursiv), wenn der rekursive Funktionsaufruf die letzte Aktion zur Berechnung von f ist. Vorteil dieser Funktionsdefinition ist, dass kein zusätzlicher Speicherplatz zur Verwaltung der Rekursion benötigt wird.
Source Wikipedia: https://de.wikipedia.org/wiki/Endrekursion
Rekursive Funktionen sollten vom Compiler effektiv optimiert werden, wenn:
int pixel_detail(int iter, COMPLEX_TYPE z,
const COMPLEX_TYPE c, const int max_iter)
{
if (iter == max_iter)
return max_iter;
z = z * z + c;
if ((z.imag() * z.imag() + z.real() * z.real() >= FLOAT_TYPE(4.0)))
return iter;
return inner(iter + 1, z, c, max_iter);
}
Keine lokalen Variablen,
die letzte Zeile enthält den rekursiven Aufruf.
| - | GCC | VS2015 |
|---|---|---|
| complex (float) | 13.3 MPixel/s | 10.8 MPixel/s |
| complex (double) | 13.2 MPixel/s | 10.7 MPixel/s |
| cmplx tail rec. (float) | 13.4 MPixel/s | 2.3 MPixel/s |
| cmplx tail rec. (double) | 13.3 MPixel/s | 5.2 MPixel/s |
| float rec. | 6.2 MPixel/s | 5.6 MPixel/s |
| double rec. | 6.2 MPixel/s | 5.7 MPixel/s |
| float tail rec. | 6.2 MPixel/s | 5.7 MPixel/s |
| double tail rec. | 6.2 MPixel/s | 5.7 MPixel/s |
mandel::Complex statt std::complex
Nette Idee - kann funktionieren - muss aber nicht
Man soll in C++ keine Schleifen selbst programmieren, sondern (STL-)Algorithmen verwenden!
Für den Mandelbrot Algorithmus ist das schwierig, da die Anzahl der Iterationen nicht vorhersehbar ist.
Aber die for-Schleifen über alle Pixel (den Bildschirm) sollte funktionieren.
Überarbeitetes Beispiel:
const int disp_width = 179, disp_height = 80;
const double start_real = -1.8, start_imag = -1.5;
const double scale_real = 3.0 / disp_width;
const double scale_imag = 3.0 / disp_height;
for (int j = 1; j < disp_height; ++j) {
for (int i = 1; i < disp_width; ++i) {
const double re = start_real + i * scale_real;
const double im = start_imag + j * scale_imag;
const int iter = pixel(re, im);
cout << transform(iter);
}
cout << '\n';
}
Bildschirmauflösung 178x79
Wertebereich: [-1.8..1.2; -1.5..1.5]
i,j: Bildschirmkoordinaten
re,im: Korrdinaten im einer Komplexen Ebende
std::vector gespeichert.(logische) Erweiterung von boost::range::iterator_range bzw. irange
template<class Integer, class StepSize>
iterator_range< range_detail::integer_iterator_with_step<Integer, StepSize> >
irange(Integer first, Integer last, StepSize step_size);
2D Integer range from array_view proposal
std::experimental::D4087::bounds<2> bnd{ width, height };
std::experimental::parallel::for_each(
std::experimental::parallel::par, std::begin(bnd), std::end(bnd),
[&](std::experimental::D4087::index<2> idx) {
const auto i = idx[0];
const auto j = idx[1];
const double re = start_real + i * scale_real;
const double im = start_imag + j * scale_imag;
const auto iter = pixel(val.real(), val.imag());
const color = transform(iter); // num iterationen -> color
...
}
Parallel STL on CodePlex
bzw. das array_view proposal:
Multidimensional bounds, offset and array_view, revision 7
ComplexRange2D<complex<double>> range{ -1.0, 1.0, -2.0, 2.0, 3, 5 };
for (const auto v : range) {
cout << v << " ";
}
cout << endl;
Wertebereich: [-1.0..1.0; -2.0..2.0]
Bildschirmauflösung 3x5 Pixel
(-1,-2) (0,-2) (1,-2) (-1,-1) (0,-1) (1,-1) (-1,0) (0,0) (1,0) (-1,1) (0,1) (1,1) (-1,2) (0,2) (1,2)
boost::irangeusing cmplx = complex<double>;
Color t(int iteration); // num iterationen -> color
vector<Color> picture(width*height);
...
ComplexRange2D<cmplx> range(
start_real, end_real,
start_imag, end_imag,
width, height);
transform(begin(range), end(range), begin(picture),
[&pixel, &t](cmplx val) {
const auto iter = pixel(val.real(), val.imag());
return t(iter);
});
Warum kein SIMD?
SIMD ist zu wichtig (für die Mandelbrot-Berechnung) um in einem Unterabschnitt abgehandelt zu werden.
Teaser:
http://benchmarksgame.alioth.debian.org/u64q/performance.php?test=mandelbrot
| Rang | Language | secs | KB | gz |
|---|---|---|---|---|
| 1.0 | Rust | 5.10 | 65,732 | 868 |
| 1.1 | C++ g++ | 5.82 | 33,964 | 726 |
| 1.2 | C gcc | 5.92 | 32,464 | 694 |
| Methode | float | double |
|---|---|---|
| Sequentiell | 12.6 MPixel/s | 12.5 MPixel/s |
| SSE | 37.6 MPixel/s | 20.3 MPixel/s |
| AVX* | 17.4 MPixel/s | 9.0 MPixel/s |
| AVX2 | 63,5 MPixel/s | 37.4 MPixel/s |
| TBB + SSE | 91.2 MPixel/s | 54.2 MPixel/s |
| TBB + AVX* | 55.9 MPixel/s | 29.7 MPixel/s |
| TBB + AVX2 | 145.0 MPixel/s | 88.9 MPixel/s |
Visual Studio 2015 | i5-5200U CPU @ 2.20GHz
c++ vector class by Agner Fog
(*) Ergebnis unerwartet
[Code-Guck] -> Bei Bedarf